John Napier e seu Calculador em Cartões

John Napier foi um Matemático e cientista que viveu no século XVII, ele descobriu os logarítimos (que posteriormente seriam cruciais na criação da régua de cálculo) e criou sistemas para facilitar a multiplicação e divisão de números longos, que diga-se de passagem hoje em dia causam pânico, imagine no século XVII. Para facilitar esses cálculos primeiramente ele adaptou um método usado em sua época, a gelosia, só que dividiu o resultado das multiplicações de cada número em barras que podiam ser colocadas lado a lado, montando assim a operação que se desejava. Este método ficou conhecido como Barras de Napier ou em inglês Napier's Bones (ossos de Napier, pois os melhores conjuntos eram fabricados em marfim).

Neste método, são necessárias parciais, ou seja, cálculos de cada dígito do número que queremos multiplicar, depois estas parciais tem que ser somadas para termos o resultado total da multiplicação. Seguindo em seus estudos, Napier inventou um método onde pode eliminar a necessidade de calcular as parciais, tendo quase que automaticamente o valor da multiplicação, bastando seguir os princípios da gelosia. Este método era constituído de um conjunto de cartões com os valores da multiplicação de 0 a 9 de um número dispostos em um quadrado dividido em 18 partes, e máscaras que deixavam a mostra somente o resultado da multiplicação pelo número que se queria.

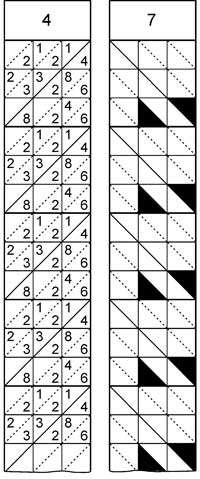
Esse conjunto de cartões foi chamado por ele de Promptuary (do latim "pronto para uso"), em inglês ficou conhecido como Napier's abacus cards, e em português por Estruturas de Napier. Com esse método, Napier revolucionou o modo como as pessoas calculavam grandes números, pois transformou a multiplicação em nada mais que uma soma.

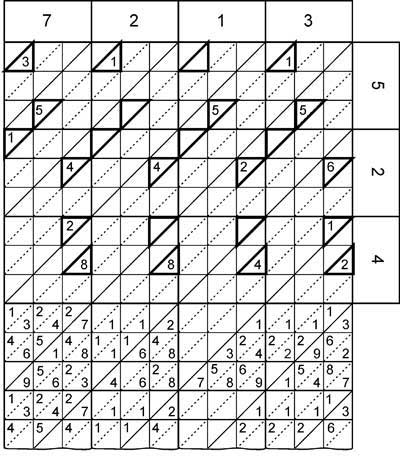
Seguindo o princípio da gelosia, basta somar os números que estão dentro da diagonal de cada dígito do nosso cálculo. No caso do exemplo acima, começando da direita para esquerda temos como último dígito na diagonal do /4/ o 2, depois na diagonal do /2/ temos (6+1+4=11) ficamos com o 1 e vai um para próxima diagonal, na diagonal do /5/ temos (5+2+8=15+1=16) ficamos com o 6 vai um  para próxima, na do /3/ temos (1+5+4+8=18+1=19) ficamos com o 9 e vai 1 para a próxima, na do /1/ temos (4+2=6+1=7), na do /2/ temos (1+5+1=7) e na do /7/ temos o número (3), lendo da esquerda para direita obtemos o número 3779612, resultado da operação (7213x524=3779612). Pode parecer complicado, mas acredite, não é.

Hoje em dia temos calculadoras que custam menos de R$ 1,00 e fazem estas operações com mais facilidade, mas no século XVII Napier conseguiu transformar estes cálculos em operações simples e rápidas, ajudando a todos que precisavam deste recurso na época. Se alguém quiser tentar, coloquei um arquivo no 4Shared, com o template das Estruturas de Napier em PDF, e se você quiser fazer modificações, tem também o arquivo em LibreOffice Draw (ODG).